为使公式能正常渲染，对部分细节有所调整，原文可点击附件查阅。

第三章课后习题

1.推导绕参考坐标系Y轴纯旋转的矩阵表示。

image-20220927172744389
图1　绕参考坐标系Y轴示意图

证明：

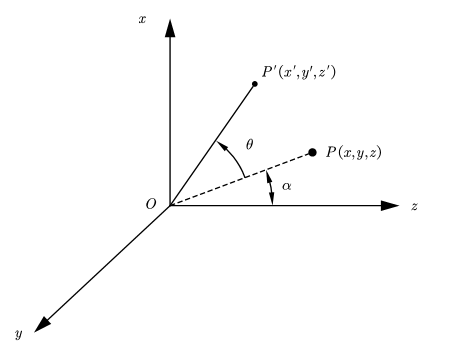
如图1所示，XYZ坐标系中，\(\overrightarrow{OP}\) 旋转\(\theta\)角到\(\overrightarrow{OP^{\prime}}\)的位置，根据三角函数关系，可以列出\(\overrightarrow{OP}\) 与\(\overrightarrow{OP^{\prime}}\)的坐标表示形式： \[ \begin{cases} z^{\prime}=\left| OP \right|\cdot \cos \left( \alpha +\theta \right) =\left| OP \right|\cdot \left( \cos \alpha \cdot \cos \theta -\sin \alpha \cdot \sin \theta \right) =z\cdot \cos \theta -x\cdot \sin \theta\\ y^{\prime}=y\\ x^{\prime}=\left| OP \right|\cdot \sin \left( \alpha +\theta \right) =\left| OP \right|\cdot \left( \cos \alpha \cdot \sin \theta +\sin \alpha \cdot \cos \theta \right) =z\cdot \sin \theta +x\cdot \cos \theta\\ \end{cases} \] 用矩阵形式重新表示为： \[ \left[ \begin{array}{c} z^{\prime}\\ y^{\prime}\\ x^{\prime}\\ \end{array} \right] =\left[ \begin{matrix} \cos \theta& 0& -\sin \theta\\ 0& 1& 0\\ \sin \theta& 0& \cos \theta\\ \end{matrix} \right] \cdot \left[ \begin{array}{c} z\\ y\\ x\\ \end{array} \right] \] 整理得： \[ \left[ \begin{array}{c} x^{\prime}\\ y^{\prime}\\ z^{\prime}\\ \end{array} \right] =\left[ \begin{matrix} \cos \theta& 0& \sin \theta\\ 0& 1& 0\\ -\sin \theta& 0& \cos \theta\\ \end{matrix} \right] \cdot \left[ \begin{array}{c} x\\ y\\ z\\ \end{array} \right] \] 证毕.

2. 推导绕参考坐标系Z轴纯旋转的矩阵表示。

image-20220927182642919
图2　绕参考坐标系Z轴示意图

证明：

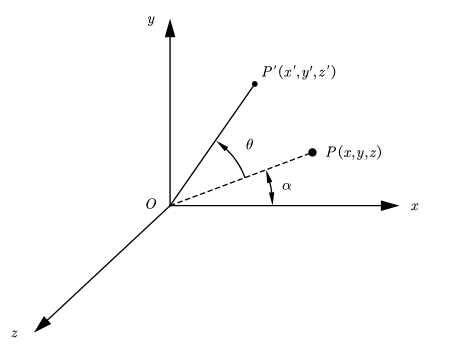
如图2所示，XYZ坐标系中，\(\overrightarrow{OP}\) 旋转\(\theta\)角到\(\overrightarrow{OP^{\prime}}\)的位置，根据三角函数关系，可以列出\(\overrightarrow{OP}\) 与\(\overrightarrow{OP^{\prime}}\)的坐标表示形式： \[ \begin{cases} x^{\prime}=\left| OP \right|\cdot \cos \left( \alpha +\theta \right) =\left| OP \right|\cdot \left( \cos \alpha \cdot \cos \theta -\sin \alpha \cdot \sin \theta \right) =x\cdot \cos \theta -y\cdot \sin \theta\\ y^{\prime}=\left| OP \right|\cdot \sin \left( \alpha +\theta \right) =\left| OP \right|\cdot \left( \cos \alpha \cdot \sin \theta +\sin \alpha \cdot \cos \theta \right) =x\cdot \sin \theta +y\cdot \cos \theta\\ z^{\prime}=z\\ \end{cases} \] 用矩阵形式重新表示为： \[ \left[ \begin{array}{c} x^{\prime}\\ y^{\prime}\\ z^{\prime}\\ \end{array} \right] =\left[ \begin{matrix} \cos \theta& -\sin \theta& 0\\ \sin \theta& \cos \theta& 0\\ 0& 0& 1\\ \end{matrix} \right] \cdot \left[ \begin{array}{c} x\\ y\\ z\\ \end{array} \right] \] 证毕.

3.求点\(P\left( 2,3,4 \right) ^T\)绕参考坐标系x轴旋转45度后，相对参考坐标的坐标。并给出Matlab程序及程序运行结果。

解： \[ P^{\prime}=\mathrm{Rot}\left( x,45^\circ \right) \cdot P=\left[ \begin{matrix} 1& 0& 0& 0\\ 0& \cos 45^\circ& -\sin 45^\circ& 0\\ 0& \sin 45^\circ& \cos 45^\circ& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \cdot \left[ \begin{array}{c} 2\\ 3\\ 4\\ 1\\ \end{array} \right] =\left[ \begin{array}{c} \begin{array}{c} 2\\ -\frac{\sqrt{2}}{2}\\ \frac{7\sqrt{2}}{2}\\ \end{array}\\ 1\\ \end{array} \right] \] Matlab程序：

1
2
3
4
5
6
7
8
9
P=[2 3 4 1]'; 
sitax=pi*45/180; 

Rotx=[1 0 0 0;
      0 cos(sitax) -sin(sitax) 0;
      0 sin(sitax)  cos(sitax) 0;
      0 0 0 1];

iP=Rotx*P

程序运行结果如图3所示.

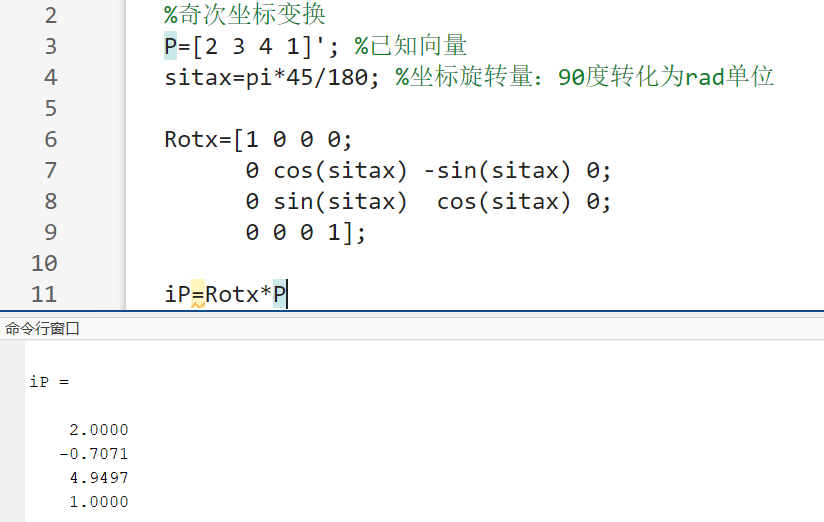
image-20220927193123112

图3　题3程序运行结果

4.求点\(P\left( 3,5,7 \right) ^T\)绕参考坐标系z轴旋转45度后，相对参考坐标的坐标。并给出Matlab程序及程序运行结果。

解： \[ P^{\prime}=\mathrm{Rot}\left( z,45^\circ \right) \cdot P=\left[ \begin{matrix} \cos 45^\circ& -\sin 45^\circ& 0& 0\\ \sin 45^\circ& \cos 45^\circ& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \cdot \left[ \begin{array}{c} 3\\ 5\\ 7\\ 1\\ \end{array} \right] =\left[ \begin{array}{c} \begin{array}{c} -\sqrt{2}\\ 4\sqrt{2}\\ 7\\ \end{array}\\ 1\\ \end{array} \right] \] Matlab程序：

1
2
3
4
5
6
7
8
9
P=[3 5 7 1]'; 
sitaz=pi*45/180; 

Rotz=[cos(sitaz) -sin(sitaz) 0 0;
      sin(sitaz) cos(sitaz) 0 0;
      0 0 1 0;
      0 0 0 1];

iP=Rotz*P

程序运行结果如图4所示.

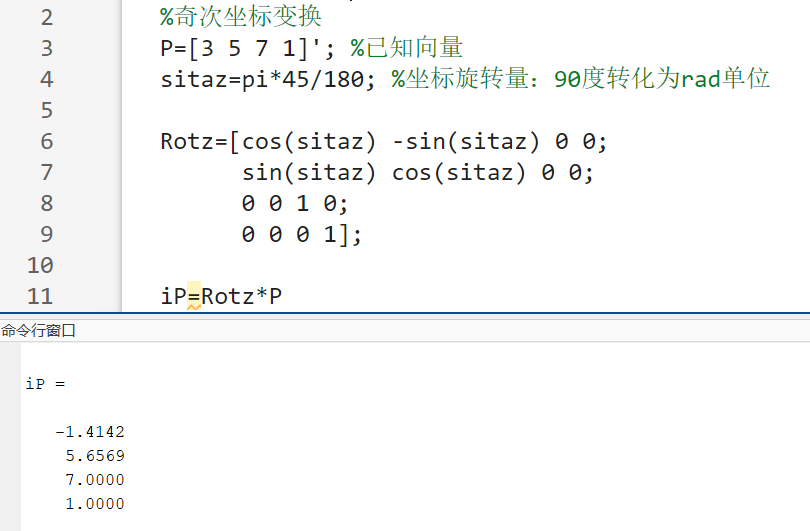
image-20220927193210810

图4　题4程序运行结果

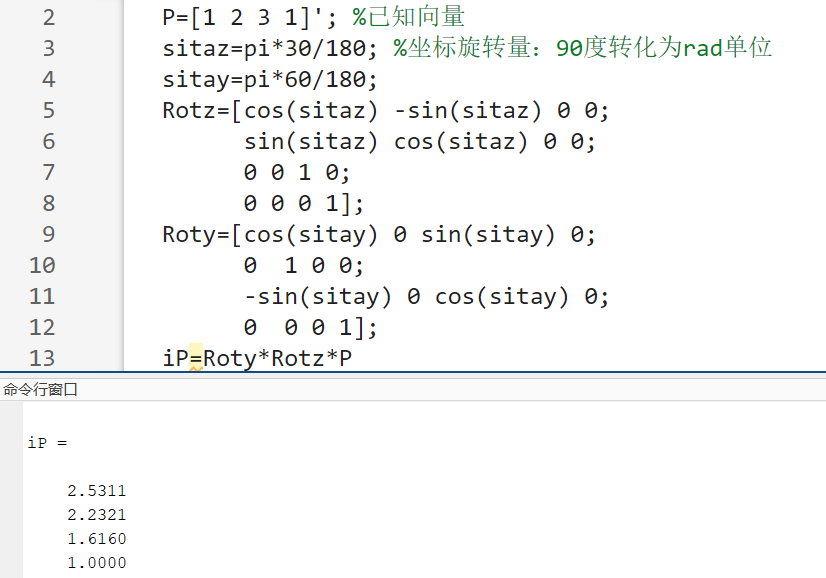
5.求点\(P\left( 1,2,3 \right) ^T\)绕参考坐标系z轴旋转30度后，再绕y轴旋转60度后，相对参考坐标的新位置。并给出Matlab程序及程序运行结果。

解： \[ \begin{aligned} P^{\prime}&=\mathrm{Rot}\left( y,60^\circ \right) \cdot \mathrm{Rot}\left( z,30^\circ \right) \cdot P\\&=\left[ \begin{matrix} \cos 60^\circ& 0& \sin 60^\circ& 0\\ 0& 1& 0& 0\\ -\sin 60^\circ& 0& \cos 60^\circ& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \cdot \left[ \begin{matrix} \cos 30^\circ& -\sin 30^\circ& 0& 0\\ \sin 30^\circ& \cos 30^\circ& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \cdot \left[ \begin{array}{c} \begin{array}{c} 1\\ 2\\ 3\\ \end{array}\\ 1\\ \end{array} \right] \\&=\left[ \begin{array}{c} \begin{array}{c} \frac{7\sqrt{3}-2}{4}\\ \frac{1+2\sqrt{3}}{2}\\ \frac{3+2\sqrt{3}}{4}\\ \end{array}\\ 1\\ \end{array} \right] \end{aligned} \] Matlab程序：

1
2
3
4
5
6
7
8
9
10
11
12
P=[1 2 3 1]';
sitaz=pi*30/180; 
sitay=pi*60/180;
Rotz=[cos(sitaz) -sin(sitaz) 0 0;
      sin(sitaz) cos(sitaz) 0 0;
      0 0 1 0;
      0 0 0 1];
Roty=[cos(sitay) 0 sin(sitay) 0;
      0  1 0 0;
      -sin(sitay) 0 cos(sitay) 0;
      0  0 0 1];
iP=Roty*Rotz*P

程序运行结果如图5所示.

image-20220927194423340

图5　题5程序运行结果

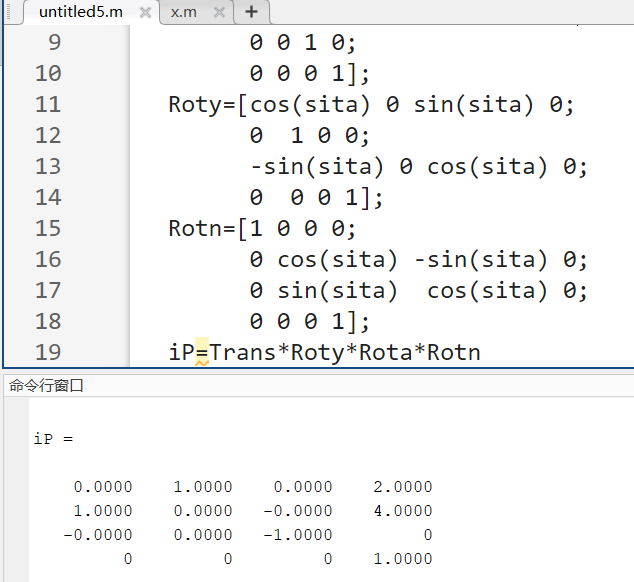
6.坐标系{B}$( n,o,a) $绕a轴旋转90度，再绕参考坐标系{i} $( x,y,z ) $的y轴旋转90度，然后沿着x轴和y轴分别移动2和4，再绕n轴旋转90度，求出该坐标系在参考坐标系内的新位姿。并给出Matlab程序及程序运行结果。

解： \[ \begin{aligned} P&=\mathrm{Trans}\left( 2,4,0 \right) \cdot \mathrm{Rot}\left( y,90^\circ \right) \cdot \mathrm{Rot}\left( a,90^\circ \right) \cdot \mathrm{Rot}\left( n,90^\circ \right) \\ &=\left[ \begin{matrix} 1& 0& 0& 2\\ 0& 1& 0& 4\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \cdot \left[ \begin{matrix} \cos 90^\circ& 0& \sin 90^\circ& 0\\ 0& 1& 0& 0\\ -\sin 90^\circ& 0& \cos 90^\circ& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \cdot \left[ \begin{matrix} \cos 90^\circ& -\sin 90^\circ& 0& 0\\ \sin 90^\circ& \cos 90^\circ& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \cdot \left[ \begin{matrix} 1& 0& 0& 0\\ 0& \cos 90^\circ& -\sin 90^\circ& 0\\ 0& \sin 90^\circ& \cos 90^\circ& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \\ &=\left[ \begin{matrix} 0& 1& 0& 2\\ 1& 0& 0& 4\\ 0& 0& -1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \end{aligned} \] Matlab程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
sita=pi*90/180; 
Trans=[1 0 0 2;
    0 1 0 4;
    0 0 1 0;
    0 0 0 1];
Rota=[cos(sita) -sin(sita) 0 0;
      sin(sita) cos(sita) 0 0;
      0 0 1 0;
      0 0 0 1];
Roty=[cos(sita) 0 sin(sita) 0;
      0  1 0 0;
      -sin(sita) 0 cos(sita) 0;
      0  0 0 1];
Rotn=[1 0 0 0;
      0 cos(sita) -sin(sita) 0;
      0 sin(sita)  cos(sita) 0;
      0 0 0 1];
iP=Trans*Roty*Rota*Rotn

程序运行结果如图6所示.

image-20220928154117445

图6　题6程序运行结果

7.圆柱坐标机器人包括两个平移运动和一个旋转运动，其顺序为：先沿x轴移动 \(r\)，在绕z轴旋转\(\alpha\)，最后沿z轴移动 \(l\)，求圆柱坐标机器人的运动变换矩阵。

解： \[ \begin{aligned} P&=\mathrm{Trans}\left( 0,0,l \right) \cdot \mathrm{Rot}\left( z,\alpha \right) \cdot \mathrm{Trans}\left( r,0,0 \right) \\ &=\left[ \begin{matrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& l\\ 0& 0& 0& 1\\ \end{matrix} \right] \cdot \left[ \begin{matrix} \cos \alpha& -\sin \alpha& 0& 0\\ \sin \alpha& \cos \alpha& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \cdot \left[ \begin{matrix} 1& 0& 0& r\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \end{aligned} \]

8.球坐标机器人包括一个平移运动和两个旋转运动，其顺序为：先沿z轴移动 \(r\)，再绕y轴旋转 \(\beta\)，最后绕z轴旋转 \(\gamma\)，求球坐标机器人的运动变换矩阵。

解： \[ \begin{aligned} P&=\mathrm{Rot}\left( z,\gamma \right) \cdot \mathrm{Rot}\left( y,\beta \right) \cdot \mathrm{Trans}\left( 0,0,r \right) \\ &=\left[ \begin{matrix} \cos \gamma& -\sin \gamma& 0& 0\\ \sin \gamma& \cos \gamma& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \cdot \left[ \begin{matrix} \cos \beta& 0& \sin \beta& 0\\ 0& 1& 0& 0\\ -\sin \beta& 0& \cos \beta& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \cdot \left[ \begin{matrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& r\\ 0& 0& 0& 1\\ \end{matrix} \right] \end{aligned} \]